›

Reference configuration for interpreting quaternion data

evanhemevanhem
in General

Hi, I would like to follow up on this post: https://mbientlab.com/community/discussion/3183/sensor-fusion-reference-frame

I tried to find the answer by searching through the forum records but came up short. Apologies if it has been addressed before.

The quaternions describe an axis-angle rotation. Every rotation needs to be described relative to some reference configuration. Without knowledge of the reference configuration, the quaternion data is useless, unless you want to use it to find angular velocities.

Is there a universal reference configuration for each sensor to properly interpret the orientation described by the quaternions? I have been doing some testing and it does not appear to be the case. I would have guessed that the quaternion (w,x,y,z) = (1,0,0,0) would correspond to a sensor lying flat on a horizontal table with its local x-axis pointing North and its y-axis pointing West (according to the local tangent plane on the Earth's surface).

However, if I play around and look at the data as it is streamed:

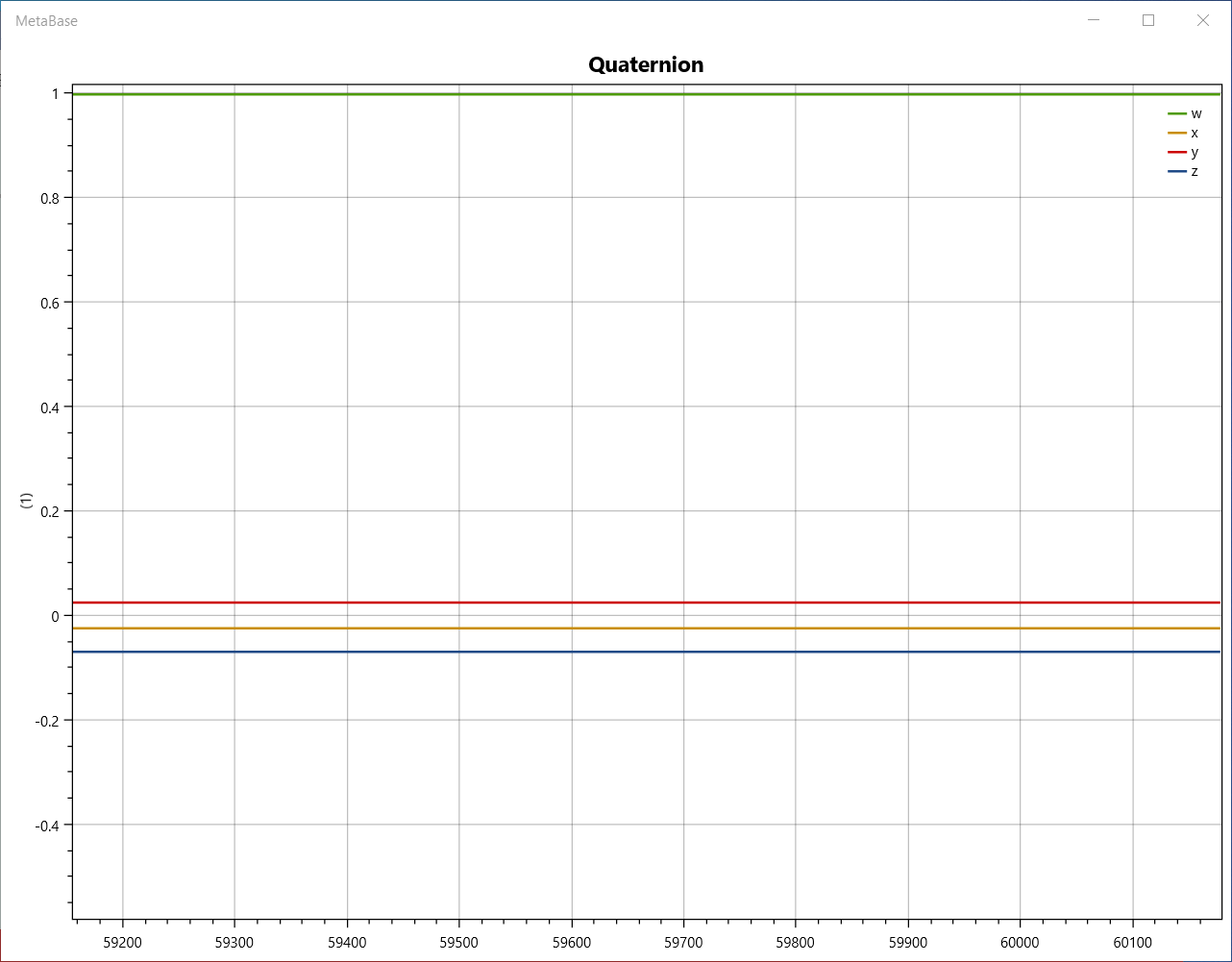
then it seems as though the reference configuration of the sensor (the configuration at (w,x,y,z)=(1,0,0,0)) is dependent on the sensor orientation at the time instance when the data starts streaming. Here is what the data looks like when I precisely find the reference configuration:

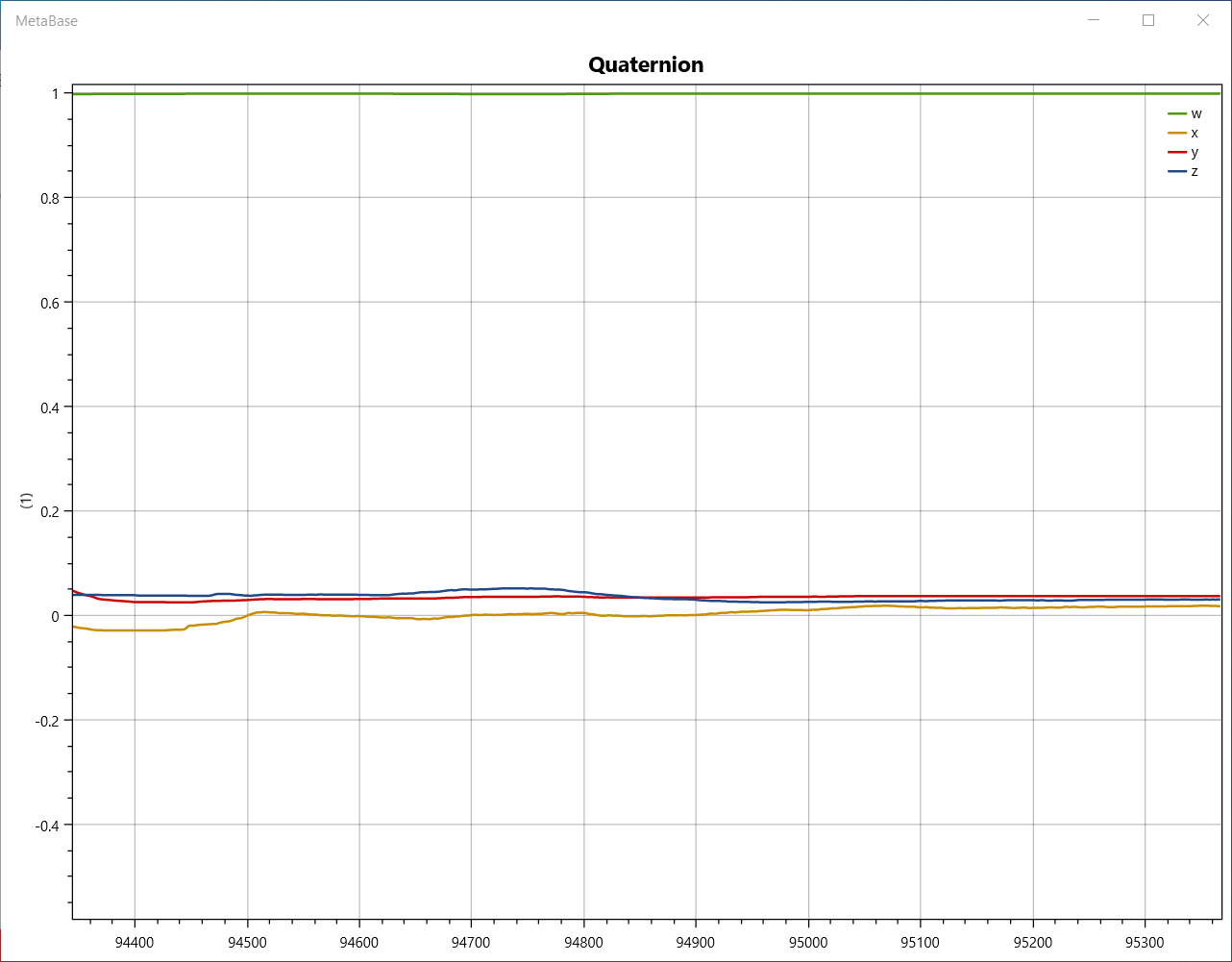
I have found in all my tests that the (w,x,y,z)=(1,0,0,0) configuration is one in which the sensor is approximately lying flat on a horizontal table. If I preserve the initial heading angle and lay the sensor flat on the table, it seems that I get close to the reference configuration. But in all experiments, this configuration is not unique, but dependent on the initial sensor configuration at the start stream time.

Can anyone confirm if this is the case?

Comments

  • LauraLaura
    edited November 2020

    Yes, all sensors are "tared" and then after that quaternions represent their changes in rotation from that start position.

    Quaternions and eulers are differential computations, not absolute. This isn't a GPS signal.

    It's your job to either set up a "tare" in software, or you can also use our Apis to calibrate the sensor in hardware/firmware.

    Please don't EVER try to understand quaternions, it is very complicated.

    In all the applications I work on, when I have to "debug", "experiment", "observe", I always change the quaternion into an euler which can be understood and "observed" in 3d for a human.

    A quaternion cannot be drawn in 3D and understood by a human easily; a euler vector can:

    (1) Euler angles are the angles of rotation of a three-dimensional coordinate frame. A rotation of Euler angles is represented as a matrix of trigonometric functions of the angles.
    (2) Quaternions are an algebraic structure that extends the familiar concept of complex numbers. While quaternions are much less intuitive than angles, rotations defined by quaternions can be computed more efficiently and with more stability, and therefore are widely used.

    Here's a fun resource: https://quaternions.online/

    In your next experiment, plot eulers, not quaternions and try to understand what is happening.

Sign In or Register to comment.