Question about ROLL angle for a sensor as produced by Euler angles and Quaternions compared.
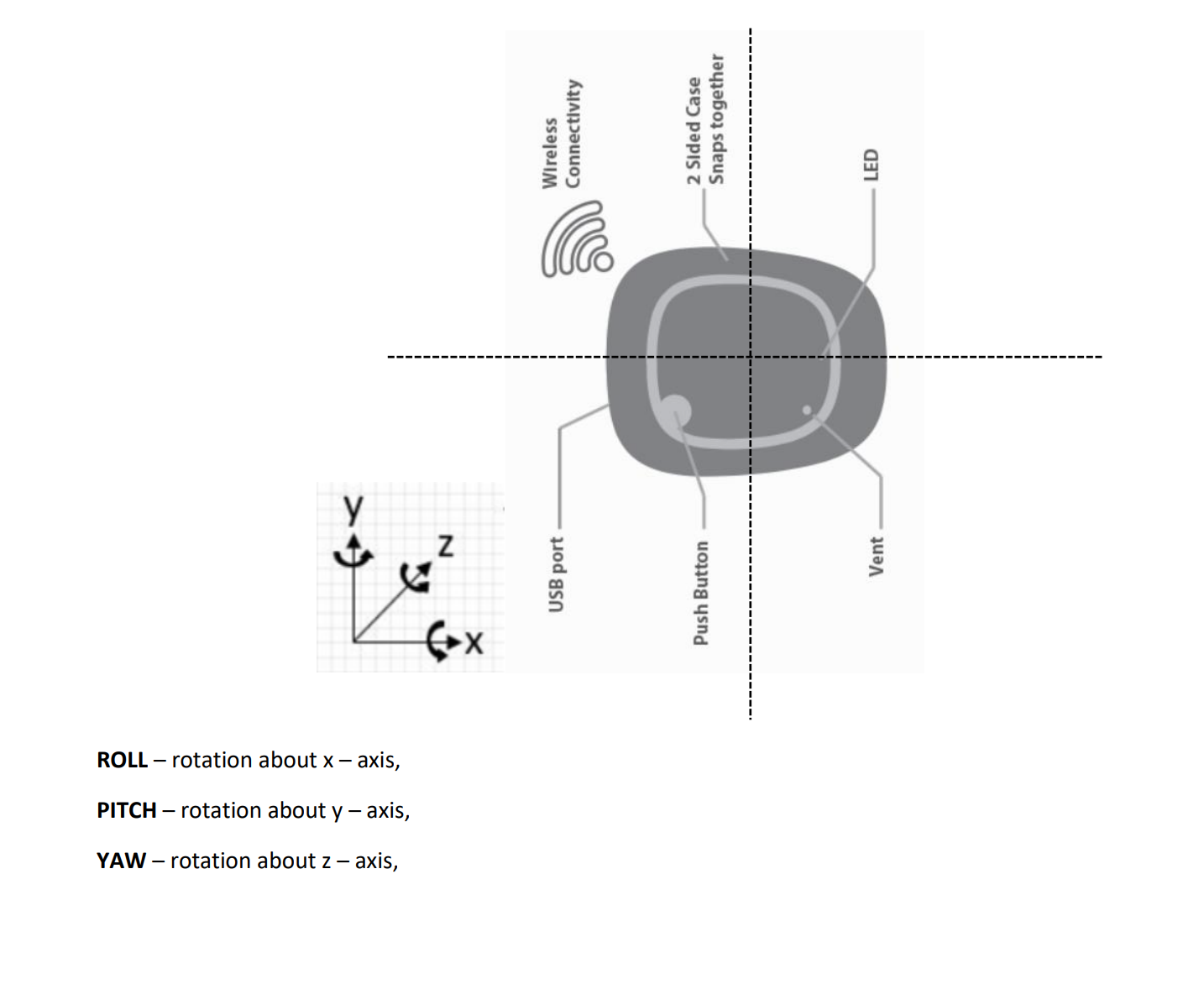
Experiment:
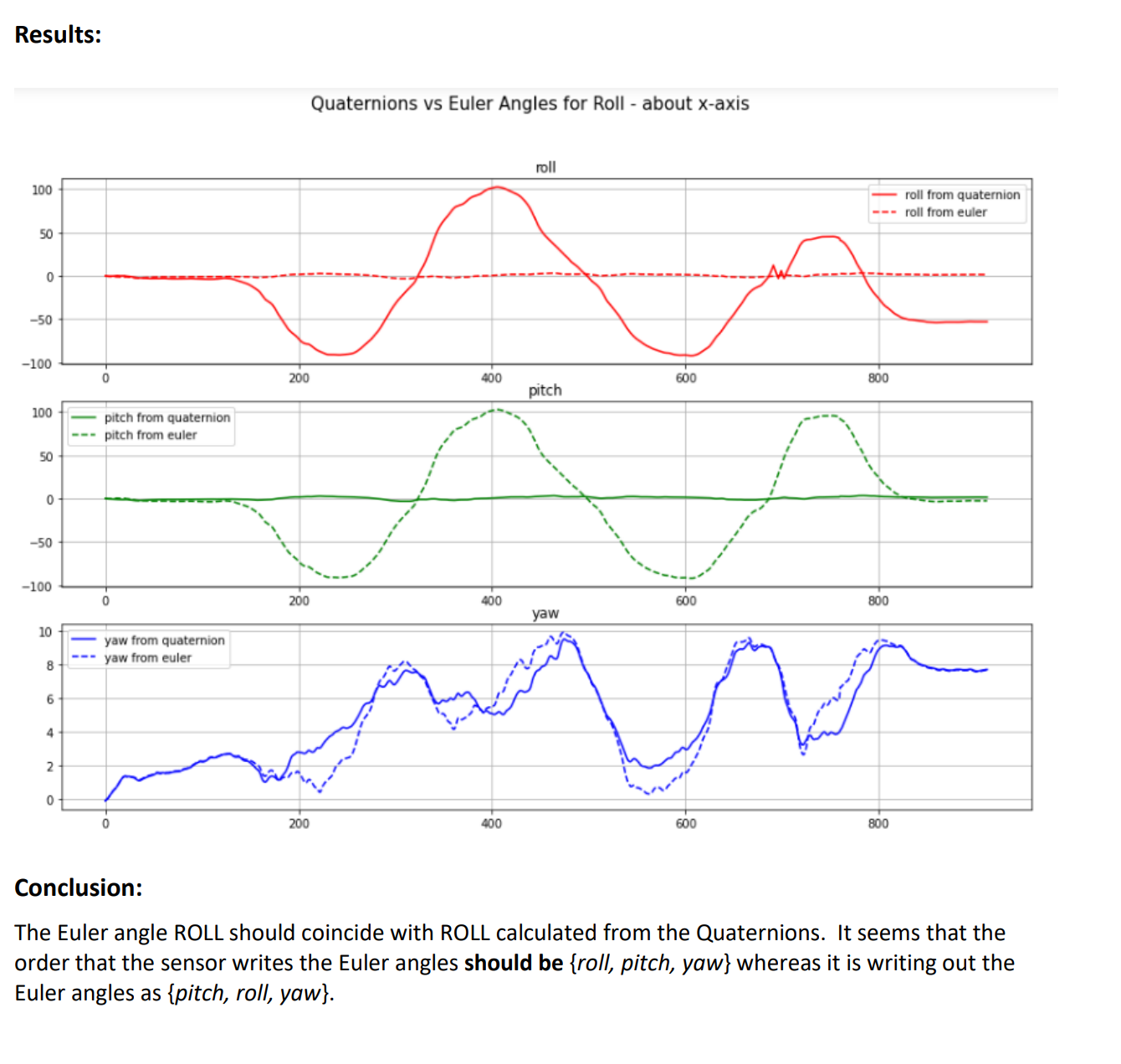
We rotated an mbient sensor around the x – axis to simulate ROLL. We collected Euler angles and
Quaternions at 100 samples/second. We calculated Euler angles from Quaternions (roll from
quaternions, pitch from quaternions and yaw from quaternions and plotted them together with the
Euler angles, roll, pitch, and yaw.
What we observe is that Euler angle PITCH corresponds with ROLL angle calculated from Quaternions
and Euler angle ROLL corresponds with PITCH angle calculated from Quaternions.
We used the following vectorized python code to convert Quaternions to Euler angles:
def quaternion_to_euler_angle_vectorized1(w, x, y, z):
ysqr = y * y
t0 = +2.0 * (w * x + y * z)
t1 = +1.0 - 2.0 * (x * x + ysqr)
X = np.degrees(np.arctan2(t0, t1))
t2 = +2.0 * (w * y - z * x)
t2 = np.where(t2>+1.0,+1.0,t2)
# t2 = +1.0 if t2 > +1.0 else t2
t2 = np.where(t2<-1.0, -1.0, t2)
# t2 = -1.0 if t2 < -1.0 else t2
Y = np.degrees(np.arcsin(t2))
t3 = +2.0 * (w * z + x * y)
t4 = +1.0 - 2.0 * (ysqr + z * z)
Z = np.degrees(np.arctan2(t3, t4))
return X, Y, Z
Comments
@awsllcjeff
Is the data you are working with from coming from one of the app's logged CSV files with named headers?
Our sensors adopted the bosch sensorfusion convention for pitch, roll and yaw, which correspond to x, y, and z axis rotations. Unfortunately, this has pitch and roll swapped from what many people consider the standard definition, though it is ultimately a convention.
So pitch (x rotation) and roll (y rotation) as reported by the sensor are swapped from how they are being calculated in your data (roll on x, pitch on y).
Have the pitch (x) and roll (y) been swapped in the latest sensor firmware (1.7.3)?
If the sensor is oriented with the x-axis pointing up (towards the sky) and I rotate the sensor about the z-axis (yaw), what should I expect to get when I convert the quaternions back to Euler angles? I do not see Euler yaw (z), I see Euler pitch (x). Why is this?
Sorry, error in my last question, corrected above:
Using firmware version 1.7.3, I notice that when I COMPUTE Euler angles from quaternions, roll (about x-axis), pitch (about y-axis) and yaw (about z-axis) CORRESPOND with the Euler angles as reported by the sensor. Was this an update that was made to version 1.7.3 of the firmware?
Please explain to me how you would convert sensor quaternions into Euler angles. I am using the following code:
def quaternion_to_euler_angle_vectorized1(w, x, y, z):
ysqr = y * y
t0 = +2.0 * (w * x + y * z)
t1 = +1.0 - 2.0 * (x * x + ysqr)
X = np.arctan2(t0, t1) * 180/np.pi
t2 = +2.0 * (w * y - z * x)
t2 = np.where(t2>+1.0,+1.0,t2)
Y = np.arcsin(t2) * 180/np.pi
t3 = +2.0 * (w * z + x * y)
t4 = +1.0 - 2.0 * (ysqr + z * z)
Z = np.arctan2(t3, t4) * 180/np.pi
With this conversion, sensor Euler angles do not match up with Euler angles calculated using sensor quaternions (as above).
Could you please explain?
Thanks!
@mhcohen56 There was no change made to sensor fusion in firmware 1.7.3.
Based on your graphs previously provided, it appears that your formula for conversion to euler angles is reasonably accurate, that is to say the waveforms are similar in shape and close to the native euler output -- with the exception that roll and pitch are swapped.
I am saying that the bosch convention coming from the sensor fusion engine defines pitch as a rotation on x, and roll as a rotation on y -- opposite of the previously posted convention. This would explain why the roll and pitch seem swapped with your calculation formula.
I would also note that euler angles are known to have some ambiguity, that is they are not guaranteed to be unique to achieve a given rotation. That may explain the slight variability in the exact yaw and roll in your graphs. When using the native euler output, I would expect it to track physical orientation better than converting from quaternions.
Regarding your question about expected euler angles with x up. This has the added complications of being essentially a gimbal lock position -- bosch definition pitch on x and yaw on z axes end up aligned. I expect this may cause further ambiguity when converting from quaternions.

It is my understanding that working with quaternions is generally preferred in computer graphics due to these issues.
Thank you Matt. How then would I use the mbient sensor to ascertain Range Of Motion (ROM) in degrees of a joint we are testing, say for example the knee?
Hi, I repeated my previous experiments with rotations about the x - axis and the y - axis separately and received contradictory results from what I posted previously. The ONLY change is that I upgraded the firmware on the sensor to version 1.7.3.
Please see the details in the attached file.
Many thanks!